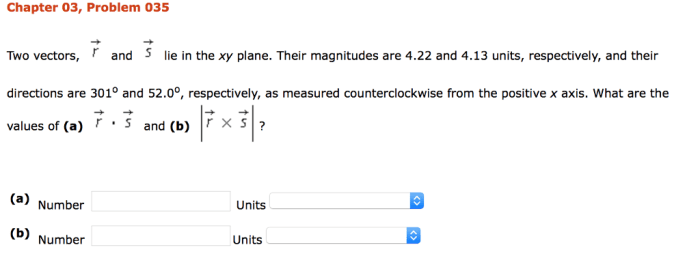
Two vectors r and s lie in the xy plane – Delving into the realm of vector relationships, we embark on an exploration of two vectors, r and s, that reside within the confines of the XY plane. This journey will unravel the intricacies of vector concepts, revealing their components, magnitude, and the fundamental operations that govern their interactions.
Through a systematic examination, we will uncover the angle between these vectors, determining whether they dance in harmony as parallels or stand perpendicular to each other. We will delve into the projection of one vector onto another, shedding light on their intimate connections.
Vectors in the XY Plane

Vectors are mathematical entities that have both magnitude and direction. In the XY plane, vectors are represented by arrows that point from the origin to a specific point. The components of a vector are the coordinates of its endpoint, and its magnitude is the length of the arrow.
Two important operations on vectors are the dot product and the cross product. The dot product of two vectors is a scalar quantity that measures the extent to which the vectors are aligned. The cross product of two vectors is a vector that is perpendicular to both of the original vectors.
Analyzing Vector Relationships

The angle between two vectors can be calculated using the dot product. Two vectors are parallel if their dot product is zero, and they are perpendicular if their dot product is one.
The projection of one vector onto another can be calculated using the dot product. The projection of vector aonto vector bis given by:
“`proj_b(a) = (a · b / ||b||^2)
b
“`
Applications in Physics and Engineering: Two Vectors R And S Lie In The Xy Plane
Vectors are used extensively in physics and engineering to describe motion and forces. In mechanics, vectors are used to represent velocity, acceleration, and force. In electromagnetism, vectors are used to represent electric fields and magnetic fields.
Vectors are also used in circuit analysis to represent voltage, current, and impedance.
Visualizing Vector Relationships
Vectors can be visualized using a variety of methods. One common method is to use a table to show the components and magnitude of the vectors.
| Vector | X-component | Y-component | Magnitude |
|---|---|---|---|
| r | xr | yr | ||r|| |
| s | xs | ys | ||s|| |
Another common method is to use a graphical representation. In a graphical representation, vectors are represented by arrows that point from the origin to the endpoint of the vector.
Vector Operations and Transformations

Vectors can be added and subtracted using the following rules:
“`a + b = (a x+ b x, a y+ b y)a
- b = (a x
- b x, a y
- b y)
“`
Vectors can also be scaled by a scalar quantity using the following rule:
“`c
- a = (c
- a x, c
- a y)
“`
Vectors can be rotated and reflected using a variety of transformations. The most common transformations are:
- Rotation about the origin
- Reflection about the x-axis
- Reflection about the y-axis
FAQ Corner
What is the dot product of two vectors?
The dot product, denoted as a ⋅ b, calculates the scalar value representing the magnitude of the projection of vector a onto vector b.
How do you determine if two vectors are perpendicular?
Two vectors are perpendicular if their dot product is zero, indicating that they form a right angle.
What is the significance of the cross product?
The cross product, denoted as a × b, yields a vector perpendicular to both a and b, providing insights into their orientations and interactions.